Extracting the signal from a coherent transmission is not easy. Luckily, technology has found the answer.
In the last part of our series on complex optical modulation, “Detection of Complex Modulated Optical Signals”, we discovered that time-domain heterodyne detectors are the most flexible detection configurations, as they can be applied on both test signals and in live, and they work regardless of the modulation format. In figure 1, this IQ detector is located on the left side. We can also see that some steps still need to be completed before the incoming bits encoded in the symbols can be identified and processed. The receiver architecture shown here is the one recommended by the Optical Internetworking Forum (OIF) and allows extracting all the information contained in the signal. Let's examine the receiver architecture further.
Solution to many problems
As an integral part of any optical receiver, digital signal processing (DSP) follows the analog-to-digital conversion. Using DSP is very useful compared to conventional on-off modulation, where we would have to worry about signal distortion effects caused by Chromatic Dispersion (CD), Polarization Mode Dispersion (PMD), etc. The DSP allows algorithms to compensate for CD, PMD and other problems, since coherent detection provides all the information in the optical field. Thus, with complex optical modulation it is no longer necessary to use PMD compensators or fibers to compensate for dispersion, nor will we suffer from the increased latency caused by these modules.
The imperfections of the receiver are eliminated with a phase of correction prior to the rise. These imperfections can be imbalances between the four electrical channels, IQ phase angle errors in the IQ mixer, desynchronizations between the four ADC channels, and a nominally balanced receiver differential imbalance. To eliminate these problems, the component is often characterized along the wavelength during instrument calibration.
In addition to the imperfections introduced by the receiver, the DSP must compensate for the degradation experienced by the signal during the optical path between the transmitter and the receiver. These can be DC and PMD, Polarization Dependent Loss (PDL), Polarization Rotation or Polarization State Transform (PST), and phase noise.
To calculate the impact of phase noise, it is possible to track the carrier phase over time. However, this step is not required in a consistent receiver configuration.
Carrier phase recovery
By introducing a local oscillator (LO), we discovered a way to monitor the phase changes of the signal over time relative to the phase of the LO. However, since in a heterodyne receiver scenario the LO has a different frequency from the signal, a linear phase shift occurs over time. This is easy to understand if we remember that in “Detection of complex modulated optical signals” we saw that in a heterodyne receiver IPhoto is proportional to the cosine of (Φ+ ωt). This "rotary" constellation can be seen in figure 2 applied to the example of quadrature phase shift keying (QPSK).
To avoid ambiguity, the phase must not change faster than π/4 per symbol time, which is equal to half the phase difference between two adjacent symbols. This, in turn, means that the frequency offset between the LO and the signal must be less than 1/8 of the symbol clock for QPSK.
To be able to track phase, the signal must be sampled at times with predictable phase values, for example, at symbol times. In the case of a bandwidth-limited signal, the phase sample rate will be less than the symbol rate. In Figure 3, the red line shows that the phase might not recover correctly.
Under these circumstances, the carrier phase offset and noise must be kept within very strict limits to allow phase recovery. However, this is often not the case in real broadcast systems, as these more stringent specifications are not required in real line cards using real-time acquisition.
Figure 4 shows the influence of the carrier bandwidth on the phase recovery of a DFB laser. An example of high tracking bandwidth is shown on the left. The constellation points on the IQ plot appear artificially narrow, since in this case the phase tracking reduces the angular width of the symbols. At a lower bandwidth, we'll get more realistic looking round symbols. And with even less bandwidth, in the carrier phase graph we have reached a limit where it is no longer possible to track the phase. The angular dispersion of the symbols is greatly affected by phase noise that could not be removed.
In search of the Jones matrix
Since we have to provide the digital demodulator with two independent baseband signals (for x and y bias), bias demultiplexing is a fundamental step in DSP. In this step, it is necessary to compensate the PMD and the PDL, and take into account that in single-mode fibers, the polarization state is not maintained during propagation.
The polarization directions evolve as the signal travels the fiber (see Figure 5), so the final state of polarization (SOP) is not simply related to the orientation of the receiver. For this reason, with the polarization beam splitter in the receiver we do not get two independent signals, but a linear combination of the two polarization tributaries. Polarization preserving fibers maintain the SOP, but are not used in data transmission due to their higher attenuation and price.
All degradation effects that occur in fully polarized light from Fiber Channel can be described mathematically with the so-called Jones matrix. The sent signal S is multiplied by the Jones matrix, obtaining the received signal R. If we had an ideal channel, without disturbances, the Jones matrix would be an identity matrix, where the received signal would be equal to the originally emitted signal (see figure 6). In its most common form, the Jones matrix is a complex 2×2 matrix with eight independent real parameters.
Thus, we have to find the Jones matrix to deduce what the original signal is from the measured received signal. This is difficult, since we usually have little or no information about the disturbing effects that the signal has suffered in the channel.
Thus, to make an approximation to the original signal, so-called blind algorithms are often used, estimation techniques for which it is not necessary to know the original signal (except in the case of modulation format). Here, a series of equalizer filters (see Figure 7), applied to the received signal, represents the inverse of the Jones matrix. Each filter serves as a model for a disturbing effect of the signal. The algorithm repeatedly searches for the set of filter variables (, ▼, k, etc.), which leads to convergence; that is, the measured symbols that map with the least error to the symbols calculated by the algorithm.
One drawback of this method is that it can recover the same bias channel twice. This problem is known as an algorithm singularity. It is also a very complex method, since each symbol must be treated individually to calculate the next step of the iteration.
Everything is simpler in Stokes space
The estimation is easier in the Stokes space, where polarization demultiplexing is really a blind procedure, since neither demodulation nor knowledge of the modulation format used or the carrier frequency is needed. Furthermore, in the Stokes space we avoid the problem of singularity.
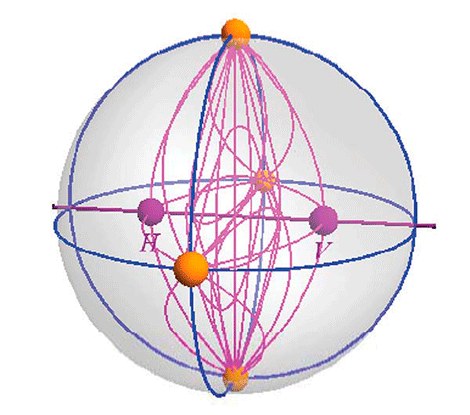
Stokes space helps to visualize the polarization conditions of optical signals, so it is also a useful tool for observing polarization changes along an optical channel. Any polarization state of fully polarized light can be represented by a point in this three-dimensional space that lies on the surface of a sphere: the so-called Poincaré sphere, which has its center at the origin of the coordinate system. The radius of the sphere corresponds to the amplitude of the light. Circular polarization can be found along the S3 axis. Along the equator in the plane that spans the S1 and S2 axes, we have linear polarization, while positions in between represent elliptical polarization. In Figure 8 we can see, in green, the situation of some specific polarization states on this globe.
Also shown in Figure 8 is a polarized QPSK signal with x and y measurements.
There are four possible phase differences between the two signals at the sampling points. Combining these x and y signals with these four phase differences gives the measured blue point clouds in Stokes space (with a QPSK signal in a single polarization direction, we would only get an accumulation on the S1 axis).
The transitions between the four states define a lens-shaped object in Stokes space (see Figure 9). Thus, it can be seen that multiplexed polarization signals of any format always define a lens of this shape.
When we look at the PST along the optical path of a single mode fiber, the lens rotates in Stokes space (see Figure 10). From this rotation we can derive the Jones matrix, which is the normal of the lens-shaped object.
But how are other disturbing effects of the signal represented in Stokes space? With Polarization Dependent Loss (PDL), the lens deforms and shifts. Even so, this does not cause problems in recovering the matrix from Jones. The deformation allows to quantify the losses dependent on the polarization. Chromatic dispersion (CD) is not dependent on polarization and does not impede polarization demultiplexing. In this case, constellation diagrams are preferable for quantitative analysis.
Determination of symbols
After a smooth DSP during polarization demultiplexing, we can finally decide on the received symbols. In QPSK, the criteria for this are the I and Q values of the measured point in the constellation diagram (see Figure 11), ie each point with a positive I and Q value will be interpreted as "11".
In more advanced formats, it is no longer possible to simply use the I and Q values for decision making. Points are assigned to the closest symbol.
From the fuzzy clouds on the right in Figure 11 we can deduce that even with coherent detection we get bit errors. Now, how to quantify them? We will cover this in the next installment of our tutorials on coherent optical signals.