Entendiendo el Cálculo del Jitter: ¿Por qué Dj puede ser menor que DDj (o Pj)?

Es una pregunta frecuente que merece una ulterior explicación. Aunque el Ritter dependiente de los datos (DDj) y el jitte periódico (Pj) son ciertamente subconjuntos del jitter determinístico (Dj) es perfectamente razonable obtener el resultado de Dj < DDj or Dj < Pj. En este artículo explicaremos como se miden DDj, Pj y Dj en un Analizdor de Datos Serie de Teledyne LeCroy y osciloscopios con SDAII o SDAIII-CompletLinQ y decribiremos como puede darse un resultado de Dj < DDj o Dj < Pj.

Introducción

El incremento de la velocidad de transmisión ha reducido el intervalo de tiempo en la unidad de transmisión o bit. La consecuencia es que en los efectos de la integridad de la señal está la creación de jitter que fácilmente pude ocasionar errores de bit. Por tanto, cuantificar el jitter se ha cobertizo en uno de los requerimientos de casi todos los protocolos de comunicaciones serie de alta velocidad. Los ingenieros deben medir la cantidad de jitter debida al transmisor y a los efectos del canal, y entender sus contribuciones al jitter total de cada una de sus componentes individuales. Los osciloscopios digitales modernos, especialmente los de gama alta, incluyen opciones de análisis de daos serie que incluyen la medida del jitter de las señales adquiridas y lo extrapolan utilizando el modelo dual-Dirac. El objetivo es predecir el impacto de eventos de jitter de muy baja probabilidad que producen bit errors a niveles mut bajos tales como 1 en 1012 .

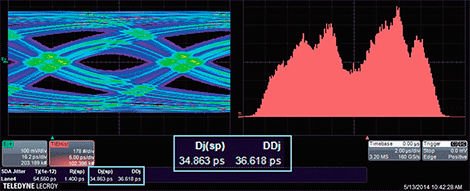
El análisis de jitter realizado por estos instrumentos puede devolver un valor de jitter determinístico (Dj) que es menor que uno de sus componentes, incluyendo el jiiter dependiente de los datos (DDj) y jitter periódico (Pj). La Figura 1 muestra un ejemplo. Para explicar por qué se puede producir esta situación, vamos a revisar los conceptos de jitter determinístico, dependiente-de-datos y periódico, ver brevemente como se miden y entonces comentar dos escenarios donde Dj < DDJ o Pj. Para una descripción mucho más detallada del método de cálculo de jitter ver la referencia [2].

Jerarquía del Jitter

La Figura 2 muestra la jerarquía del jitter aceptada en la industria. El jitter total se divide en dos componentes: aleatorio y determinístico, que tienen los atributos de ser ligados o no respectivamente. El Jitter Determinístico (Dj) se divide a su vez en dos grupos: Relacionados con el patrón de datos o no. El jitter que es ligado y correlacionado a los datos es “Data dependent jitter” (DDJ). Todo el jitter que está ligado pero no relacionado al patron de datos va al saco llamado “BUJ”, incluyendo el jitter periódico (Pj). En la figura 2 es fácil ver que el jitter data-dependiente y el periódico son subconjuntos del jitter determinístico. Aún así es factible que Dj < DDj or Pj.. ¿Como puede se posible?

¿Qué es el Jitter Determinístico?

El jitter determinístico se define como el jitter que está ligado a la señal y el entorno con un bien definido alcance máximo y mínimo. Esto es en contraste con el jitter aleatorio, que es Gaussiano por naturaleza, y no está ligado a una fuente estable y concreta. Hay una gran variedad de fuentes determinísticas incluyendo dependiente de datos /DDj) y periódico (Pj). La Figura 3 muestra una distribución de jitter debido puramente a un agresor a jitter periódico que es una simple sinusoide. El jitter periódico es generado por relojes u otras fuentes periódicas que pueden modular los pulsos transmitidos y en le caso de un jitter senoidal con una frecuencia provoca una distribución en forma de bañera. (De todas formas no veremos este histograma idealizado en una señal real por la inevitable presencia de cambios en la distribución debidas al jitter aleatorio, tal como veremos después.) Hay que destacar que el histograma de la figura tiene un rango muy bien definido: está ligado. Por tanto este jitter es determinístico.

¿Cómo se calcula el Jitter Determinístico (Dj)?

En los analizadores de datos seri de alta gama, el Dj se calcula realizando un ajuste al modelo de jitter dual-Dirac. En este contexto, el Dj se escribe de forma mucho más precisa como Dj(delta-delta) o Dj(δδ).De hecho, la nomenclatura utilizada para describir Jitter Determinístico es una fuente de confusión. Cuando solo se escribe como “Dj”, como es generalmente el caso, no es “Dj(peak-peak)” y puede ser fácilmente y generar confusiones.

El modelo dual-Dirac describe jitter como dos funciones delta Dirac convolucionados con una Gaussiana. La figura 4 muestra una imagen de la formulación del modelo dual-Dirac. Las funciones delta μL y μR anteriores modelan el jitter determinístico. Su separación en el tiempo (μL – μR) es Dj(δδ). La distribución Gaussiana (curva punteada) modela el jitter aleatorio. Dj(δδ) está determinado por el ajuste de la función acumulativa de distribución (CDF) del jitter por la fórmula Tj(BER) = alpha(BER) * Rj + Dj(δδ). Alpha es un multiplicador basado en la selección del usuario del VER. Por ejemplo, para un BER=10- 12, alpha=14,07. Para más información del modelo dual-Dirac ver las referencias finales.

Conceptualmente la función del modelo es realizar la predicción del jitter teniendo en cuenta un gran conjunto de datos, p.ej. >1012 unidades de intervalos. Para realizar esta tarea el modelo extrapola los extremos del jitter aleatorio para modelar su desarrollo. (Los rotos en la curva sólida muestra como el jitter aleatorio se extrapola). Como más de 1012 intervalos es mucho mayor que lo que puede adquirirse con un osciloscopio en un breve periodo de tiempo, muchos comités de estándar de datos serie han estandarizado con el modelo dual-Dirac para determinar Tj(BER), Rj and Dj(δδ).

El punto clave aquí es que Dj(δδ) no se calcula sumando componentes individuales de jitter determinístico. En su lugar es un ajuste a un modelo. Consecuentemente Dj(δδ) no es una medidad “peak-to-peak” o “full scale”.

Muchos ingenieros encuentran de hecho que Dj(δδ) no sea una medida peak-to-peak confuso y quieren tener un valor Peak-to-peak para Dj. Hallar Dj(peak-peak) sin un conocimiento previo de todos los agresores del jitter determinístico puede ser muy complicado y difícil. Por ejemplo, mirando el histograma de jitter de la Figura 5, Como querrías eliminar el componente de jitter aleatorio para obtener un valor peak-to-peak de Dj? Puede parecer sencillo en el histograma de la izquierda pero muy complicado en canales con distribución compleja del jitter como en la derecha.

Qué es Data-Dependent Jitter?

Las características eléctricas de un canal pueden provocar que el jitter observado sea dependiente del patrón de datos transmitido. Por ejemplo, el jitter en el último flanco de una secuencia de bits 00001 puedes ser diferente del de una secuencia 11101. Reflexiones y pérdidas dependientes de la frecuencia en el canl causan este comportamiento llamado Inter-symbol interferente (ISI). LA Figura 6 muestra un ejemplo de ISI. La traza roja es la señal. La traza azul es la forma de onda del “jitter track”. El jitter-track muestra el jitter medido en el tiempo con la señal adquirida. Se nota que el jitter track muestra un patrón repetitivo al igual que la señal. Cada bit en el patrón tiene un valor de jitter que depende de los bits previos. ISI es un tipo de jitter determinístico y está ligado como en el ejemplo del jitter periódico mostrado en la Figura 3. De todas formas, el jitter está correlacionado al patrón de datos, y es por tanto “data-dependent-jitter”. Por último, el otro tipo de jitter dependiente de los datos es el debido a las variaciones en el nivel de cruce utilizado para determinar los tiempos del flanco, un Offset en la amplitud de la señal o aimetrías en los tiempos de subida/bajada. Este tipo de deterioro de la señal es duty-cycle distorsion (DCD).

¿Como se calcula el Jitter Dependiente de los Datos (DDj)?

A diferencia del cálculo de Dj(δδ), que se realiza en dos pasos extrapolación y ajuste, DDj se calcula directamente de los datos adquiridos. Para una señal que es un patrón repetitivo, las medidas de error del intervalo de tiempo se analizan por evidencia de la reptición del patrón. El Histograma DDj de la Figura 7 muestra la distribución resultante del jitter. El rango de escala total de esta distribución es el DDj. DDj se divide en ISI y DCD; Las medidas de ISI y DCD se derivan del análisis de los histogramas de DDj utilizando flancos positivos y/o negativos. Ver referencia [2] para ver más información. DDj es una medida “full-scale” o “Peak-to-peak”. Ya que DDj es ligado, utilizar una medida pk-pk para DDj es la aproximación correcta. Por tanto, la medida resultante de DDj no incluye ningún jitter desligado.

¿Qué es el Jitter Periódico?

Como se ha mencionado anteriormente, el jitter periódico se produce por relojes u otras fuentes periódicas que pueden modular los pulsos transmitidos. El subsiguiente jitter track oscila como puede verse en la Figura 8.

Cuando el Pj de un contribuyente sinusoidal domina sobre todos las otras fuentes de jitter se observa una distribución con forma de bañera. En presencia de otras fuentes de jitter como el aleatorio, ISI o múltiple Pj puede ser imposible ver la forma de bañera. De todas formas le jitter track suele mostrar evidencias claras de un agresor de jitter periódico. La Figura 8 muestra el jitter track e histograma de dos señales que están sufriendo de jitter periódico con algún jitter aleatorio mezclado.

¿Como se calcula el Jitter Periódico?

Para aislar el jitter periódico de otras fuentes, primero se “corta” el jitter dependiente de datos usando promediado del pattern para generar el jitter track conteniendo solo jitter aleatorio y ligado pero no relacionado a datos )incluyendo Pj). Un análisis espectral de la señal de track permite hallar y aislar los picos de Pj del ruido de fondo en el espectro del jitter. La extensión Peak-peak de la inversa de FFT de los contribuyentes de Pj son el Pj resultante. La Figura 9 muestra un ejemplo.

Dj(oo) puede ser menor que DDj o Pj

Ya que Dj(oo) es un ajuste a un modelo y no una simple medida a fondo de escala como DDj o Pj, debería estar claro que comparar Dj(oo) con DDj y Pj debe realizarse con cautela. Si Dj fuese una medida a fondo de escala (ej. “Dj(pk-pk)”), entonces DDj y Pj serían siempre menores que Dj. Esto sería cierto “por definición” ya que DDj y Pj son subconjuntos de Dj en la jerarquía del jitter. Sin embargo, en el modelo dual.Dirac, Dj no está definido com Dj(pk.pk) sino como Dj(oo) que es un modelo dependiente de parámetros con la consecuencia de que Dj(oo) puede ser menor que DDj o Pj.

En general los modelos solo se corresponden con la realidad hasta un determinado punto. La distribución de jitter de las señales del mundo real, casi nunca es igual a la distribución del modelo dual-Dirac. Este hecho es suficiente para concluir que Dj(oo) no será igual que Dj(pk-pk). Pero, ¿por qué, en genera, es Dj(oo)

Cuando la distribución del jitter determinístico incluye una población significativa en el interior de los extremos, como en la Figura 10, entonces la convolución del jitter aleatorio gaussiano y la distribución del jitter determinístico produce un PDF (y subsecuentemente un CDF) lo que es pobre para ajustar al modelo dual- Dirac. La consecuencia es que cuando el ajuste Tj = alpha * Rj + Dj(δδ) se realiza, Dj(δδ) toma un valor que está a distancia del valor actual de Dj(Peak-peak). La Figura 10 muestra este efecto. La distribución superior muestra una lata relación de Pj a Rj. Como la cantidad de jitter aleatorio se incrementa, la convolución de las distribuciones (Gaussiana para jitter aleatorio y seno PDF para el jitter periódico) lleva los picos hacia dentro. Consecuentemente cuando DDj (o Pj) es la fuente principal del jitter determinístico se produce Dj(oo) < DDj (o < Pj), y Dj(oo) < Dj(peak-peak). El hecho de que el ajuste al modelo dual-Dirac se realice en los extremos de la distribución también causa que sea bastante sensitivo a la cantidad de datos adquiridos. Es importante adquirir unas señales suficientemente largas y número de repeticiones del patrón para evitar estadísticas insuficientes.

Ejemplo #1: Dj< Pj

La Figura 11 muestra un resultado de un escenario donde Dj(oo) < Pj.La tabla de jitter muestra los resultados: Dj = 1.27 ps, Pj = 1.47 ps. Es una señal simulada que puede ser potencialmente la salida de un reloj con un jitter muy bajo, pero que está afectado de un acoplamiento de un agresor periódico externo.

La Figura 12 muestra la distribución debida meramente a jitter periódico (verde) comparado con el actual PDF(rojo). Como el modelo dual-Dirac está basado en dos funciones delta, uno puede esperar el ajuste de las funciones delta sea cerca de los dos máximos de la distribución roja, como ilustra la distribución debida a la contribución del Oj solo. El resultado es que Dj(oo) < Pj. (Nota; Las escalas verticales de los dos histogramas no son representativas de su población relativa).

Ejemplo #2: Dj< DDj

La Figura 13 muestra el escenario donde Dj(oo) < DDj. La tabla de jitter muestra los resultados: Dj(oo) = 34.97 ps, Pj = 36.706 ps. La distribución del jitter total muestra los efectos de la convolución de ISI con jitter aleatorio. Claramente, la distribución es un ajuste terrible al modelo dual-Dirac, y la distribución del jitter muestra como si hubiera muchos picos individuales. El análisis de patrones se utiliza para entender el alcance del DDj. La Figura 7 muestra el histograma de DDj superpuesto a la distribución del jitter total. Por la misma razón mostrada en el ejemplo 1, Dj(δδ) queda valorado por debajo de DDj; las posiciones de las dos funciones Dirac quedan metidas hacia dentro ya que la distribución es pobre para realizar el ajuste con el modelo dual-Dirac.

Validez del Modelo Dual-Dirac

Uno puede preguntarse, “¿Por qué utilizar el modelo Dual-Dirac si no es suficientemente bueno para las distribuciones de jitter del mundo real?” Hay varias maneras de contestar esta pregunta. Una respuesta “fácil” es desde la perspectiva de los fabricantes de instrumentación: “Porque los clientes requieren que el osciloscopio utilice este modelo”. Otra respuesta, no completamente satisfactoria es “ No hay ninguno mejo aceptado por la industria”.

Incluso con sus limitaciones, el modelo es suficientemente útil y cubre las necesidades de los estándares. El modelo está bien definido y estandariza el método para entender el jitter total y está relacionado con la probabilidad de la aparición de un bit de error. Evita utilizar un resultado peak-to-peak para determinar el jitter total, que es una buena elección, ya que los resultados Peak-to-peak dependen excesivamente de la cantidad de datos adquiridos y es aleatorio debido a la naturaleza independiente del jitter aleatorio y no predice la cantidad total de jitter para un nivel específico de VER. El modelo Dual-Dirac puede utilizarse en diferentes tipos de instrumentos tales como osciloscopio de tiempo real, osciloscopios de tiempo equivalente (de muestreo) y testers de Bit error.

Conclusión

El jitter determinístico es una medida que es fácilmente mal entendida. Los ingenieros a menudo quieren describir jitter determinístico Peak-to-peak, pero determinarlo no es fácil, especialmente en presencia de distribuciones complejas de jitter causadas por ISI y Pj. En cambio el jitter determinístico se cuantifica por el modelo dual-Dirac, con el modelo dependiente de resultados Dj(oo). Ya que la convolución Gaussiana representado el jitter aleatorio con el jitter determinístico puede colocarse en las localizaciones de las funciones Dirac delta, Dj(oo) < Dj(peak-peak). Cuando el jitter determinístico está dominado por el jitter dependiente de los datos DDj (tipicamente debido a ISI) o por el jitter periódico Pj, entonces se pueden producir las desigualdades Dj(oo) < DDj, Dj(oo) < ISI y Dj(oo) < Pj.

Descargar PDF