Cuando surge un problema de compatibilidad electromagnética (CEM), o de interferencias electromagnéticas (EMI), o cuando debemos diseñar un nuevo equipo, donde debemos decidir cómo diseñar su circuito impreso o decidir el tipo de cable a usar en cada tipo de señal, o debemos decidir el tipo de caja o blindaje a usar, hay dos variables principales a tener en cuenta. Estas variables determinan muchas decisiones técnicas. Éstas son la frecuencia máxima de la señal circulante por cada conductor (cable, pista o conector) y su amplitud de tensión o de corriente. En cada zona del equipo, área del circuito impreso, cable, conector, etc, es necesario determinar los valores de amplitud de la señal (tensión e intensidad) y su frecuencia máxima. En el diseño de CEM, la longitud de onda del armónico de mayor frecuencia de cada señal es la que determina muchos detalles de las soluciones a decidir en cada problema de CEM.
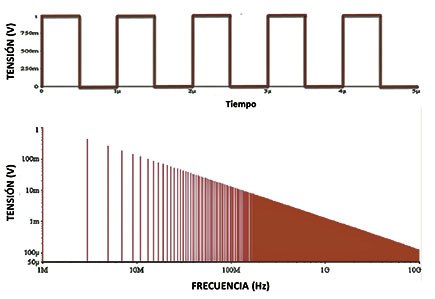
Hay dos formas principales de ver una señal. Cada forma proporciona una perspectiva diferente. Las diferentes perspectivas que se utilizan para mirar las señales se llaman dominios: el dominio del tiempo y el dominio de la frecuencia. El dominio del tiempo es el mundo real, es el único dominio que realmente existe. El dominio de la frecuencia es una entelequia matemática que nos ayuda en el análisis de las señales. El osciloscopio en el dominio del tiempo y el analizador de espectros en el dominio de la frecuencia son los dos instrumentos más útiles para identificar, caracterizar y solucionar los problemas de CEM en un equipo. En una gran mayoría de casos, los problemas de CEM se identifican mejor usando el analizador de espectro en el dominio de la frecuencia. Si el problema está relacionado con oscilaciones, resonancias, o diafonía en señales digitales, el uso del osciloscopio es más práctico, en el dominio del tiempo. La aplicación del Análisis de Fourier es una herramienta clave para analizar las señales relacionadas con los problemas de CEM. Las Series de Fourier nos permiten cambiar la representación discreta de una señal en el dominio del tiempo, mientras que la Transformada de Fourier se usa normalmente para analizar señales continuas a nivel digital. Aunque en muchos documentos se habla de ondas cuadradas en sistemas digitales, en realidad se trata siempre de ondas trapezoidales, al tener tiempos de conmutación de subida y bajada no iguales a cero. Cuando tenemos varios valores de frecuencia, la colección de sus amplitudes se llama espectro. Cada forma de onda en el dominio del tiempo tiene un patrón particular de su espectro. La única manera de calcular el espectro de una forma de onda en el dominio del tiempo es con la Transformada de Fourier. La figura 1 presenta una onda cuadrada ideal con su espectro de frecuencias. En ella los tiempos de conmutación son cero, por definición. La figura 2 muestra una señal cuadrada ideal junto a una señal trapezoidal y sus espectros de frecuencia comparados. Las envolventes del espectro de una onda trapezoidal real envuelven todo el contenido de las señales que típicamente se encuentran en la resolución de los problemas de EMI o CEM en los sistemas digitales. Los tiempos de conmutación (de subida tr y de bajada tf ), la anchura de los impulsos y la simetría del impulso o grado de simetría (“duty cycle”) tienen una gran influencia en el contenido espectral y sus amplitudes. También afecta la frecuencia fundamental. Conociendo estos parámetros se puede estimar el nivel de los armónicos y sus frecuencias para poder plantear su filtrado adecuado.
La figura 3 presenta el cálculo de la envolvente del espectro de una onda trapezoidal simétrica (por simplicidad), típica en las señales digitales. Para ello debemos conocer sus parámetros determinados por la tecnología de los circuitos integrados usados en el equipo (tr y tf), la frecuencia y la simetría y amplitud de la señal para poder calcular todos sus armónicos, para saber el impacto de los armónicos de más alta frecuencia en las emisiones conducidas y radiadas. Notar que el grado de simetría d (%) determina el primer punto de inflexión, (1 / π d) mientras que el tiempo de conmutación tr determina el segundo punto de inflexión (1 /π tr) en la envolvente, cambiando la pendiente de caída desde 0 dB/década a -20 dB/década (punto de inflexión 1), y de -20 dB/década a -40 dB/década (punto de inflexión 2), respectivamente. En realidad, la envolvente del espectro de frecuencias envuelve los lóbulos que forman los armónicos, como se ve en la figura 4, donde se ilustra que un incremento del tiempo de subida tr (0,1 a 0,5 ns) determina una menor magnitud de armónicos. Notar que la línea de la envolvente también baja junto con el nivel de los lóbulos azules correspondientes a tr2 = 0,5 ns. La figura 5 muestra que reduciendo el valor del grado de simetría d (%) se reduce el nivel de la magnitud de la envolvente (línea verde), reduciendo el nivel de los armónicos de mayor frecuencia. Conociendo la frecuencia fundamental, tr y d sabremos el contenido armónico de las señales de un circuito, sobre todo los armónicos de más alta frecuencia como en el caso del reloj.
Definición de los tiempos de conmutación
El tiempo de conmutación es el tiempo que tarda la señal (tensión o corriente) en hacer la transición desde el valor bajo al valor lógico alto o al contrario. Hay dos formas de definirlo. El tiempo de subida 10%-90% es el tiempo que tarda la señal en la transición del 10 % de su valor final al 90 % de su valor final. Éste suele ser el significado predeterminado y más usual del tiempo de subida.
La segunda definición es el tiempo de subida 20%-80%. Este es el tiempo que tarda la transición desde el 20% de su valor final al 80 % de su valor final. Por supuesto, para la misma forma de onda el tiempo de cambio 20%-80% es más corto que el tiempo de subida 10%-90%. Algunos fabricantes usan la definición 20%-80% en sus componentes. Pero puede ser confuso. Para eliminar la ambigüedad, a menudo es una buena práctica hacer referencia explícita al tiempo 10%-90% o al tiempo 20%-80% , y así evitar confusiones.
Dominio del tiempo y dominio de la frecuencia
La cualidad más importante del dominio de la frecuencia es que no es real. Se trata de una construcción matemática. La única realidad es el dominio del tiempo. El dominio de la frecuencia es un mundo matemático que sigue reglas muy específicas. La regla más importante en el dominio de la frecuencia es que el único tipo de formas de onda que existen son las sinusoidales. Hay cuatro propiedades que hacen que las ondas sinusoidales sean muy útiles para describir cualquier forma de onda. Estas propiedades son las siguientes:
1. Cualquier forma de onda en el dominio del tiempo puede ser completamente descrita de forma única por combinaciones de ondas sinusoidales.
2. Dos ondas sinusoidales cualquiera con diferentes frecuencias son ortogonales entre sí. Si se multiplican juntas y se integran en el tiempo, su valor es cero. Esto significa que se puede separar cada componente de todas los demás.
3. Están bien definidas matemáticamente.
4. Tienen un valor en todas partes, sin valores infinitos y tienen derivadas que no tienen valores infinitos. Esto significa que estos valores pueden ser usados para describir cualquier forma de onda del mundo real, ya que en el mundo real no hay valores infinitos.
La única razón por la que es bueno cambiar a otro dominio es para analizar