Muchos diseñadores de hardware usan, por inercia desde hace años, condensadores de desacoplo de 100 nF, sin analizar las frecuencias involucradas en su placa de circuito impreso (PCI). Este valor se usa desde hace tiempo, pero sólo es válido para frecuencias por debajo de los 40 MHz. Hoy en día hay muchos diseños que exceden estas frecuencias en sus señales y por ello se debe reconsiderar el valor a usar en los condensadores de desacoplo.
La tecnología electrónica ha cambiado mucho en los últimos 20 años, aumentando la frecuencia de trabajo y reduciendo los tiempos de conmutación de las señales digitales. Ello obliga a replantearse las técnicas de diseño del trazado de las pistas de los circuitos impresos junto con las estrategias de desacoplo, para asegurar la integridad de las señales y el cumplimiento de los requerimientos de compatibilidad electromagnética (CEM).
Es importante comprender que decidir los condensadores de desacoplo no es solo el proceso de localizar condensadores adyacentes a los circuitos integrados (CI) o en la fuente de alimentación, para que las corrientes transitorias debidas a las conmutaciones queden filtradas.
Se trata del proceso de seleccionar sus valores, sus dieléctricos y sus localizaciones condensadores de forma coherente con el diseño del bus de alimentación desde la fuente de alimentación hasta llegar a cada uno de los circuitos a desacoplar.
Frecuencias y tiempos a considerar
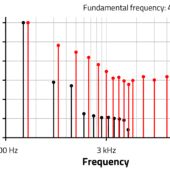
Para diseñar el sistema de desacoplo en nuestra PCI debemos considerar s sus frecuencias máximas y los tiempos mínimos de conmutación de las señales que van a circular por ella. Pero, a efectos de la integridad de las señales y de la compatibilidad electromagnética, en este análisis, es más importante considerar los tiempos de subida y bajada mínimos de las señales digitales que la frecuencia fundamental máxima. Por ejemplo, la frecuencia del reloj del microcontrolador o de alguna otra señal de mayor frecuencia en nuestra PCI que usualmente tendrán los tiempo de conmutación más pequeños. Para empezar la tarea vamos a considerar, como ejemplo fácil, una onda trapezoidal simétrica y veremos su contenido harmónico y su envolvente.
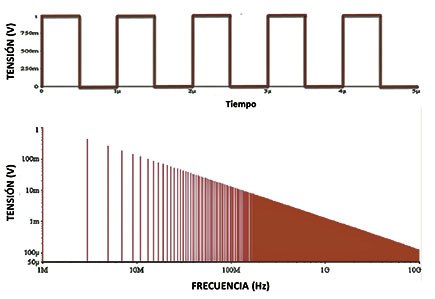
La figura 1 muestra su espectro de Fourier y la fórmula de cálculo para esta onda trapezoidal simétrica. En el caso usual donde el tiempo de subida tr = ts es mucho menor que el periodo T de la señal, la envolvente de los armónicos decrece con una pendiente de -20dB/década hasta el punto f = 1 / π tr , a partir del que la pendiente aumenta a -40 dB/década. A partir de este punto, la amplitud de los harmónicos siguientes decrece considerablemente. Esto muestra que conforme el tiempo de subida decrece, la energía de los harmónicos de mayor frecuencia aumenta.
Debemos tener en cuenta que la energía de los harmónicos de la señal de mayor frecuencia, normalmente con el menor tiempo de conmutación, nunca superará esta envolvente. Así pues, esta envolvente nos ayuda a conocer los límites máximos posibles de todas las frecuencias de todos los harmónicos de todas las señales circulantes en nuestra PCI.
Por ejemplo, con un tr = 1 ns, el punto de inflexión queda en: f = 1 / π tr = 1 / π 1*10¯9 9= 318,3 MHz.
En señales LVDS, donde tr = 300 ps, se llega a anchos de banda de 1 GHz. Conviene pues seleccionar la tecnología con la menor frecuencia de las señales y con los mayores tiempos de subida que sea posible.
Los diseñadores de software tienden a querer disponer de las máximas frecuencias de reloj posibles de las CPU más rápidas sin considerar las consecuencias en el diseño de hardware relativas a la CEM y a la integridad de las señales. De forma práctica, seria conveniente considerar hasta el 7º harmónico como mínimo en los cálculos. Por ejemplo, para una frecuencia de 50 MHz de reloj, deberíamos considerar frecuencias de cómo mínimo 350 MHz en la PCI. Los diseñadores de software tienden a querer disponer de las máximas frecuencias de reloj posibles de las CPU más rápidas sin considerar las consecuencias en el diseño de hardware relativas a la CEM y a la integridad de las señales. Para ponderar esta tendencia conviene que los diseñadores de hardware seleccione la tecnología con la menor frecuencia de las señales y con los mayores tiempos de subida que sea posible.
Los condensadores de desacoplo y sus conexiones
En el diseño de la placa de circuito impreso, un aspecto importante a considerar es la estrategia del sistema de desacoplo general, donde se deberá tener en cuenta las frecuencias, los tiempos de conmutación de las señales y el comportamiento real de los condensadores.
Cualquier condensador real siempre tiene unos elementos parásitos (resistencia serie (ESR) e inductancia serie (ESL). El elemento parásito más importante a tener en cuenta es su inductancia serie interna, junto con la inductancia serie debida a sus conexiones a la PCI.
La figura 2 muestra las gráficas de la impedancia en función de la frecuencia, de un condensador ideal, un condensador real y un condensador real soldado en una PCI. En el condensador real, el circuito LC equivalente tiene una frecuencia de resonancia:
fr = 1 / 2 π √ LC
La impedancia característica de un condensador real es
w = 1 / √ LC
A partir de la frecuencia de resonancia, el comportamiento del condensador cambia según sea ideal o real. En el condensador ideal, la impedancia característica sigue siendo mínima a partir de la frecuencia de resonancia. En el condensador real, en cambio, la reactancia inductiva se vuelve importante y el condensador deja de comportarse como una capacidad y es equivalente a una inductancia. En la frecuencia de resonancia la impedancia característica es muy baja y igual a la resistencia serie equivalente (ESR), al anularse entre si las reactancias capacitiva e inductiva, al ser iguales y de signo contrario. La ESR tiene valores muy bajos, del orden de 0,4 Ω. Debido a este valor tan bajo, en la frecuencia de resonancia, la efectividad del desacoplo es máxima.
Por debajo de la frecuencia de resonancia, el condensador real se comporta como tal, correctamente. El condensador, al ser conectado a la PCI añade la inductancia serie de las conexiones y desplaza hacia abajo la frecuencia de resonancia. De aquí que sea importante conectar el condensador a la PCI con pistas muy cortas para mantener su frecuencia de resonancia lo más alta posible. Por encima de la frecuencia de resonancia el circuito es inductivo y su impedancia se incrementa con la frecuencia.
La inductancia interna de un condensador de desacoplo de montaje superficial tiene un valor de 1 a 2 nH. Teniendo en cuenta la inductancia de las conexiones de las pistas de la PCI y sus vías, se añaden de 5 a 20 nH o más, dependiendo de su trazado. Una vía estándar tiene aproximadamente 0,7 nH. Además, las conexiones internas en el circuito integrado (CI), hasta llegar al “die” de silicio pueden tener de 3 a 15 nH de inductancia, dependiendo del tipo de encapsulado del CI. Las inductancias de las pistas en la PCI están bajo el control del diseñador. Es importante reducirlas trazando estas pistas lo más cortas y lo más anchas que sea posible, de forma que el condensador tenga la mínima inductancia total serie. Así pues, vemos que la inductancia serie puede variar entre 10 nH y 40 nH, aunque típicamente puede quedar en un margen de 15 a 30 nH. Como hemos visto antes, esta inductancia es la que limita la efectividad de los condensadores de desacoplo.
La figura 3 muestra la impedancia en función de la frecuencia de varios condensadores de desacoplo (100, 10 y 1 nF) cuando se conectan cada uno en serie con unas pistas de 12 mm. Las líneas de puntos muestran cómo sería el comportamiento de los condensadores ideales donde su impedancia decrece continuamente al incrementar la frecuencia, asumiendo que no tienen inductancia serie. Las líneas sólidas muestran el comportamiento de los condensadores reales de montaje superficial (SMD), teniendo en cuenta su inductancia serie total, sumando la inductancia de sus conexiones. Los puntos de menor impedancia son los correspondientes a las frecuencias de resonancia de cada uno de los condensadores con sus conexiones. El condensador de 100 nF tiene en estas circunstancias una frecuencia de resonancia de unos 4 MHz, que es demasiado baja. El condensador de 10 nF llega a los 30 MHz, que es todavía baja considerando las frecuencias típicas de hoy en día. El condensador de 1 nF llega un poco por encima de los 100 MHz, más aceptable. Realizando un mejor trazado, acortando las pistas para reducir la inductancia serie, podemos obtener una frecuencia de resonancia mayor. Así pues, vemos que disponiendo de un solo condensador de desacoplo de 100 o 10 nF al lado del circuito integrado, no es un método efectivo para desacoplar circuitos digitales a frecuencias por encima de los 40 MHz.
Pero no se debe cometer el error de pensar que el condensador es totalmente inefectivo a partir de la frecuencia de resonancia simplemente porque la inductancia domina su impedancia. Dado que la impedancia total es menor que la impedancia sin el condensador presente, el condensador aporta un cierto nivel de desacoplo que se puede aprovechar.
Estrategias de desacoplo
El ruido localizado en la alimentación debido a las conmutaciones digitales y sus harmónicos puede causar problemas de integridad y demasiada emisión electromagnética. Las posibles soluciones para el desacoplo de alta velocidad pueden ser:
• Disminuir los tiempos de subida y bajada de las señales digitales (difícil).
• Reducir las corrientes de los transitorios (difícil).
• Reducir la inductancia serie de los condensadores de desacoplo y sus conexiones (factible).
• Usar múltiples condensadores de desacoplo (fácil).
Las dos primeras soluciones no aportan una diferencia significativa con las nuevas tecnologías de alta velocidad y por tanto son un soluciones débiles y difíciles de acometer.
Reducir la inductancia serie en el condensador de desacoplo es una mejor solución, pero por sí misma no resuelve el problema del desacoplo a alta frecuencia. Si observamos la tabla siguiente, veremos que incluso con una inductancia de 10 nH (difícil de realizar) y un condensador de 1 nF, se tendría una frecuencia de resonancia de 50 MHz. Por ello, no es posible mover la frecuencia de resonancia con un simple condensador real y su conexión a unas frecuencias por encima de 50 MHz.
A frecuencias por debajo de la frecuencia de resonancia, las consideraciones más importantes son tener suficiente capacidad para aportar la carga para el requerido transitorio de corriente de la conmutación y tener una impedancia suficientemente baja para cortocircuitar el ruido generado por las conmutaciones.
Por encima de la frecuencia de resonancia, lo más importante es tener baja inductancia, para tener baja impedancia para que la red LC de desacoplo siga siendo suficientemente efectiva.
Un simple condensador de desacoplo no aporta suficiente baja inductancia. Por ello la solución real a alta frecuencia consiste en usar múltiples condensadores. Hay tres posibilidades de actuación:
• El uso de múltiples condensadores, todos con el mismo valor.
• El uso de múltiples condensadores, con dos valores diferentes.
• El uso de múltiples condensadores con varios valores diferentes, usualmente espaciados entre ellos una década.
Múltiples condensadores con el mismo valor
Cuando se conectan múltiples redes LC en paralelo, con condensadores del mismo valor, la capacidad total es igual a: Ct = n C , donde C es la capacidad de un condensador y n el número de condensadores en paralelo o redes LC. La inductancia total es: Lt = L / n , donde L es la inductancia serie de cada condensador y sus conexiones y n el número de redes LC. Esta ecuación es correcta sólo si la inductancia mutua es negligible en comparación con la inductancia de cada red LC. Para evitar la inductancia mutua, estas redes LC deben estar físicamente separadas. De las ecuaciones anteriores se deduce que aumentando el número de redes LC se aumenta el valor de capacidad y se disminuye el valor de inductancia, lo cual mejora las prestaciones del desacoplo.
Los requerimientos para un desacoplo efectivo con redes LC en paralelo son los siguientes:
• Poner todos condensadores con el mismo valor y así compartirán la corriente transitoria por igual.
• Cada condensador debe alimentar el CI de forma independiente, a través de diferentes pistas separadas para evitar la inductancia mutua, porque podría aumentar el valor de inductancia.
La figura 4 muestra los efectos del uso de 10 condensadores reales idénticos de 10 nF, asumiendo que comparten un pequeño plano de alimentación para tener un buen conexionado, en comparación con un solo condensador real de 10 nF. Usando idénticos condensadores se evitan los problemas de las resonancias en paralelo o anti-resonancias que ocurren cuando se usan condensadores con diferentes valores, como se verá más adelante.
La figura 5 muestra la impedancia en función de la frecuencia para varias redes LC idénticas en paralelo, (1, 8 y 64 condensadores) donde en todos los casos la capacidad total es igual a 1 µF. Como resultado, la impedancia a bajas frecuencias queda muy reducida, menor a 0,2 Ω desde 1 MHz a 1 GHz. Con 64 condensadores la impedancia es menor a 0,5 Ω desde menos de 1 MHz a 350 MHz. El uso de un gran número de condensadores con igual valor es un medio efectivo para obtener una baja impedancia de desacoplo y es efectivo en un amplio margen de frecuencias. Esta estrategia es muy efectiva cuando se usan grandes encapsulados en los circuitos integrados.
Múltiples condensadores de dos valores distintos
En algunos casos se puede recomendar el uso de dos valores distintos de condensadores de desacoplo basándonos en la teoría de que el valor grande de capacidad es efectivo a frecuencias bajas y el valor pequeño es efectivo a altas frecuencias. Si se usan dos valores distintos de condensador, tendrán dos frecuencias de resonancia distintas según la figura 6, lo cual en principio, es bueno. A pesar de que esto es verdad, cuando dos condensadores de diferentes valores se disponen en paralelo, puede surgir un problema de resonancia paralelo o anti-resonancia, que ocurre entre las dos redes LC de desacoplo. La figura 6 presenta la impedancia de un condensador de 100 nF en paralelo con uno de 10 nF, ambos con una inductancia serie de 15 nH, donde se presentan dos frecuencias de resonancia producidas por las dos redes LC, una a unos 4 MHz y la otra sobre los 13 MHz. No obstante, hay un pico de resonancia paralelo o de anti-resonancia sobre los 10 MHz, lo cual es malo. Este efecto está causado por la anti-resonancia entre las dos redes. El cálculo de la frecuencia de anti-resonancia usa la misma ecuación que la frecuencia de resonancia serie, presentada antes. La figura 7 muestra porque ocurre esto. En ella se presentan dos redes LC con diferentes valores de condensador, conectados entre los planos de alimentación y masa. Debemos asumir que C1 es mucho mayor que C2 y que las dos inductancias son iguales. Por debajo de la frecuencia de resonancia f < fr1, las dos redes son capacitivas y la capacidad total es la suma de C1 y C2, pero prácticamente es similar al valor mayor C1. Por ello el condensador pequeño C2 prácticamente no tiene efecto en la red de desacoplo. Por encima de la frecuencia de resonancia f > fr2, ambas redes son inductivas y la inductancia total es igual a las dos inductancias en paralelo o sea la mitad de la inductancia, si están separadas para que no tengan inductancia mutua, ya que haría aumentar su valor. Esto mejora el desacoplo a frecuencias por encima de fr2. A frecuencias situadas entre las dos frecuencias de resonancia de las dos redes, la red con el mayor condensador es inductiva y la red con el menor condensador es capacitiva. El circuito equivalente de las dos redes es por ello un condensador en paralelo con una inductancia y esta red en paralelo provoca un pico de anti-resonancia. La forma, amplitud y localización dependerá de la diferencia entre valores de los condensadores, su ESL, su ESR y su conexionado. Si los dos valores tienen un ratio de dos a uno, la amplitud del pico resonante quedará reducida a un valor aceptable. El mayor problema surgirá cuando los condensadores tengan diferentes valores en un orden de magnitud o más. Por ello podemos concluir:
• La red del condensador pequeño no tendrá prácticamente efecto en las prestaciones del desacoplo a frecuencias por debajo de fr1.
• El desacoplo mejorará a frecuencias por encima de fr2, porque la inductancia decrecerá.
• El desacoplo será realmente peor en algunas frecuencias entre las dos frecuencias de resonancia debido al pico de frecuencia anti-resonante, lo cual es indeseable.
• Por ello no hay una mejora sustancial en las prestaciones del desacoplo a altas frecuencias cuando se añade un condensador de bajo valor. De hecho, las prestaciones de desacoplo son peores entre 50 y 200 MHz.La figura 8 muestra la impedancia en función de la frecuencia de 4 redes de desacoplo LC. Para comparar, son una con 10 condensadores idénticos en paralelo (igual a la figura 4) y las otras están formadas por condensadores de 100 nF, 10 nF y 1 nF SMD, cada uno con una Inductancia serie total de 2 nH. Entre las frecuencias de resonancia de los tres condensadores pueden surgir picos de anti-resonancia. Si se usan condensadores iguales, esta indeseable posibilidad desaparece.
Múltiples condensadores con varios valores distintos
En algunas circunstancias es recomendable el uso de bastantes condensadores con varios valores espaciados típicamente por décadas, aplicando la teoría de que las múltiples impedancias producidas por las frecuencias de resonancia de los diferentes valores son una ventaja, porque aportarán una baja impedancia en un mayor rango de frecuencias. Sin embargo, cuando se usan condensadores de desacoplo con varios valores pueden aparecer picos de anti resonancia.
La figura 9 presenta estas resonancias y anti-resonancias usando 10 condensadores con valores entre 100 y 1 nF, localizados adecuadamente para obtener una reducción de su inductancia equivalente a L/n. Se sigue presentando con los 10 condensadores idénticos en paralelo (igual a la figura 4). Para comparar se muestra claramente que usando 10 condensadores iguales y cercanos se consigue tener una menor impedancia que usando la red conjunta de valores de 1 a 100 nF (por debajo de 12 MHz y desde 60 a 150 MHz). Por encima de 150 MHz, la impedancia de ambas alternativas es igual. Como se puede observar se producen anti-resonancias en varios puntos. Si algunos harmónicos del reloj del sistema están cerca de las frecuencias de estos picos, el ruido en el bus de alimentación se incrementa. También se debe notar que la amplitud de los picos anti-resonantes se incrementa con la frecuencia.
Al fin, la recomendación sería usar varios condensadores, pero todos con el mismo valor ya que esta configuración trabaja bien y tiene menos puntos de anti-resonancia que el uso de múltiples valores distintos.
Considerando el concepto de usar un gran número de condensadores con igual valor llevado al límite, se puede concluir que la capacidad de desacoplo sería un número infinito de condensadores de valor infinitesimal en lugar de usar condensadores discretos.
Esto es equivalente a disponer un plano de alimentación por encima de un plano de masa, lo cual tiene un valor práctico de 15 pF /cm2. Pero este valor de capacidad es insuficiente por encima de 50 MHz. Por ello se debe incrementar el valor de capacidad, reduciendo el espacio entre planos o incrementando la constante dieléctrica del circuito impreso, o como se debe hacer siempre, añadiendo condensadores de desacoplo.
Jerarquía en el sistema de desacoplo
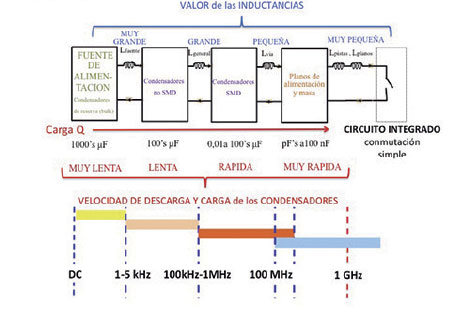
A nivel de placa de circuito impreso (PCI) se debe establecer una jerarquía en la estructura del sistema de desacoplo. La figura 10 presenta el diagrama de bloques de la estructura de desacoplo a nivel de PCI. Desde la fuente de alimentación hasta cada unos de los circuitos integrados, donde se tienen las conmutaciones digitales, los valores de las inductancias de las conexiones entre cada uno de los bloques va disminuyendo. Así vemos que las inductancias que deben ser las menores posible son las situadas entre el condensador más cercano y el circuito integrado y entre los planos de alimentación y masa y el CI. Conforme nos alejamos del CI, el valor de la inductancia va aumentando dentro de unos límites aceptables: Lplanos < Lpista < Lvia < Lgeneral < Lfuente. Desde la fuente de alimentación hasta el CI, los valores de los condensadores usados en cada uno de los bloques de desacoplo va disminuyendo. Por el contrario, la velocidad de descarga de estos condensadores va aumentando con frecuencias desde la corriente continua hasta 1 GHz.
En cada bloque de desacoplo se debe considerar el tipo de desacoplo de los explicados anteriormente, dependiendo de las frecuencias a desacoplar partiendo de los correspondientes tiempos de subida tr, en función de las tecnologías usadas. La carga Q hacia los condensadores no viaja desde la fuente de alimentación directamente al CI a alta velocidad y por ello es necesario establecer esta jerarquía de desacoplo.
En cada nivel de desacoplo, siempre la descarga es más rápida que la carga de los correspondientes condensadores. Para poder ejecutar una conmutación, la carga necesitada por el CI la toma de los planos de alimentación y masa (que forman un condensador distribuido) y de su de bloque de condensadores más cercano.
Este bloque se recarga del bloque de condensadores anterior y así sucesivamente hasta llegar a la fuente de alimentación. Los valores de capacidad conviene que sean lo más altos posible dentro del encapsulado escogido para optimizar el tener unas bajas ESR y ESL, con el máximo valor de capacidad.
Si los condensadores se sitúan una al lado del otro deben alternar sus conexiones a la alimentación y a masa para así reducir la inductancia global. La configuración de conectarlos a la alimentación y masa todos en la misma dirección tiene mayor inductancia.